A partir de determinado diámetro de tubería, las piezas especiales como codos, tes, etc, se convierten en un problema. Llegando a ser un problema serio en el momento en que tienen que ser fabricados ex profeso. Ciertamente, se trata de un problema serio, relativamente, puesto que hoy en día existen herramientas que nos permiten diseñar y construir estas piezas especiales.
Sin embargo, todo se va complicando conforme aumentamos el diámetro de la conducción y/o la presión. De cualquier forma, en este artículo, vamos a tratar el desarrollo de codos angulares o codos a inglete, para el trazado en campo de los mismos.
Codos angulares o a inglete
Los codos angulares o codos a inglete son piezas realizadas mediante gajos de tubería. Se trata de gajos rectos. Normalmente los codos angulares o a inglete empiezan a ser necesarios en tuberías a partir de diámetro 600 mm. Empiezan a ser necesarios porque o bien para esas medidas ya no existen o bien, porque son excesivamente caros.
Los codos angulares se fabrican por regla general en acero a partir de chapa, aunque también se puede hacer a partir de la propia tubería. La ventaja de hacerlo de chapa es que se puede pedir la chapa cortada según nuestras necesidades. Mientras que si se hace de tubería, se puede aprovechar restos y se ahorra soldadura, ya que no es necesario realizar la soldadura longitudinal, solamente, la soldadura entre gajos.
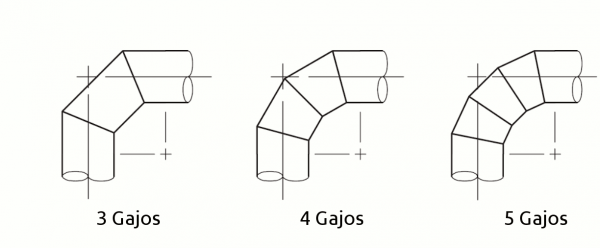
Como veremos mas adelante un codo angular o a inglete de 90º se puede fabricar a partir de dos gajos hasta cinco gajos (o mas). El número de gajos dependerá de la normativa a la que ciñamos la fabricación por un lado, y de la pérdida de carga que queramos conseguir en el codo. Como te puedes imaginar, a mayor número de gajos, la pérdida de carga producida por un codo a angular o a inglete será menor.
Desarrollo de codos angulares o a inglete
Para el desarrollo de codos a inglete, he utilizado dos normativas
- Norma UNE EN 10224. Tubos y accesorios en acero no aleado para el transporte de líquidos acuosos, incluido agua para consumo humano
- El manual de diseño M11 de la AWWA. Steel Pipe. A guide for Design and Installation.
Número de gajos
De estas dos normas de referencia, sin lugar a dudas, la guía M11 es mas restrictiva que la UNE, haciendo las siguiente distribución:
- Para angulo ≤ 22.5º -> 2 gajos
- Para 22.5º < angulo ≤ 45 º -> 3 gajos
- Para 45º < angulo ≤ 67.5 º -> 4 gajos
- Para 67.5º < angulo ≤ 90 º -> 5 gajos
Para los mismos supuestos, la UNE EN 10224, nos indica lo siguiente:
- Para angulo ≤ 30º -> 2 gajos
- Para 30º < angulo ≤ 60º -> 3 gajos
- Para 60º < angulo ≤ 90º -> 4 gajos
Radio de curvatura
Por otro lado, la guia M11, indica que el radio del codo debe ser como mínimo 2,5 veces el diámetro del tubos, \( R = 2.5 D \). Nuevamente la norma UNE es mas laxa en este sentido, donde para tubos de diámetro mayor o igual a 457 mm, el radio de curvatura R no debe ser inferior a 1,0 D. Para cualquier otra condición el radio de curvatura R no debe ser inferior a 1,5 D.
Espesor del codo
En cuanto al espesor del tubo, la norma UNE no hace ninguna indicación respecto a su dimensionamiento, sin embargo la guia M11, permite calcularla a través de la siguiente ecuación:
$$ t = \frac{P D}{S f}[\frac{S}{2}+\frac{D}{3}tan{\frac{\Theta}{2}}] $$
donde:
- t es el espesor del codo (mm)
- P es la presión interna de diseño (MPa)
- f es la tensión de diseño admisible a la presión de diseño (mm)
- D es el diámetro interior de la tubería (mm)
- S es la longitud de un segmento interior del codo (mm)
Teniendo en cuenta que la longitud del segmento anterior se puede calcular a través de la siguiente ecuación:
$$ S = 2(R – \frac{D}{2})tan{\frac{\Theta}{2}} $$
sustituyendo en la ecuación anterior:
$$ t = \frac{P D}{S f}[1+\frac{D}{3 R – 1.5 D}] $$
Llegados a este punto solo queda determinar las coordenadas de cada vértice del codo. Esto es tan sencillo como utilizar estas ecuaciones:
- R es el radio del codo
- G es el numero de gajos
- n es el vertice a calcular
- \( \alpha \) es el angulo del codo
- \( X_c \) es la coordenada x del centro del codo
- \(Y_c \) es la coordenada y del centro del codo
El primer vértice se calcula con las siguientes ecuaciones:
$$ X_1 = X_c+R $$
$$ Y_1 = Y_c $$
Para el resto de puntos las ecuaciones son las siguientes:
$$ X_n = X_{n-1} – 2 R tan (\frac{\alpha}{2(G-1)})*sen (\frac{\alpha}{G-1}(n-2)) $$
$$ Y_n = Y_{n-1} + R tan (\frac{\alpha}{2(G-1)})*cos (\frac{\alpha}{G-1}(n-2)) $$

Gracias por los datos, excelente blog
gracias alguna vez fui dibujante , y realizaba estos trazos de fabricación de codos en gajos ahora a los 64 años ya no recordaba como hacerlo y gracias a esta pagina puedo realizar nuevamente estos trazos
de verdad felicidades y gracias
Excelente
Hola gracias por el aporte.Estoy por hacer unos codos en chapa de 2mm ,de 90° diámetro interno de 61cm, 66cm y 76 cm. Son para rotomoldeo de plástico. Normalmente los codos plásticos que compró en diámetro 65 y 75 cm tienen 7 gajos 5 gajos grandes y 2 más chicos que van en cada extremo. Me pueden ayudar a hacer los cortes de los gajos?
Hola Gracias por el aporte . Como sería para hacer los gajos de codos grandes de diámetros de 76cm , 66cm y 61 cm. Sería para hacer codos de 90° en chapa de 2mm estos mismos serían para hacer rotomoldeo de plástico. Normalmente los codos plásticos que compró en diámetro 75cm y 60cm son de 7 gajos 5 gajos grandes y 2 chicos 1 en cada extremo. Me podrían ayudar con el trazado de los gajos? Por ejemplo en el plástico el codo diámetro 75cm puedo notar que los gajos en la parte más ancha miden 30cm y en la parte más corta 10cm .
Datos muy claro y concisos. Muy buena las puntualizaciones.