Para la completa definición de una placa de orificio necesitamos realizar el cálculo mecánico. Es necesario que seamos capaces de asegurar que el espesor del que vamos a dotar a la placa es suficiente. No solo para que resista a las solicitaciones a las que va a verse sometida la placa de orificio, sino, también para asegurar que las deformaciones producidas por estas solicitaciones no van a afectar al correcto funcionamiento de la placa. Todo ello con independencia del uso que le vayamos a dar a esa placa, ya sea para utilizarla como medidor de caudal como para limitar la cavitación en otros elementos de la propia conducción.

En artículos anteriores, he comentado como realizar el dimensionamiento de la placa de orificio desde el punto de vista de las condiciones hidráulicas a las que va a verse sometida. Igualmente, he definido la geometría de la placa de orificio, mas conveniente para una mejor medida de caudal. Además tienes a tu disposición  Jole, una herramienta implementada para Android con la que realizar todos estos cálculos.

Con todo ello, vamos a dar una vuelta de tuerca más al cálculo y diseño de placas de orificio. Vemos como determinar el espesor de una placa de orificio.

Determinar el espesor de una placa de orificio

Como he comentado en la introducción, en este artículo vamos a definir el espesor de las placas de orificio desde el punto de vista mecánico. Para ello, vamos a seguir el procedimiento descrito en el libro Theory of plates and shells de Stephen Timoshenko y S. Woinowsky–Krieger.

Procedimiento de cálculo

En el capítulo 3 Symmetrical bending of Circular Plates, apartado 17, Circular Plate with a Circular Hole at Center, resuelve varios casos de placas circulares con un orificio centrado sometido a diferentes solicitaciones. Desde placas simplemente apoyadas con a placas empotradas, y solicitaciones que van desde cargas puntuales a cargas uniformente distribuidas.

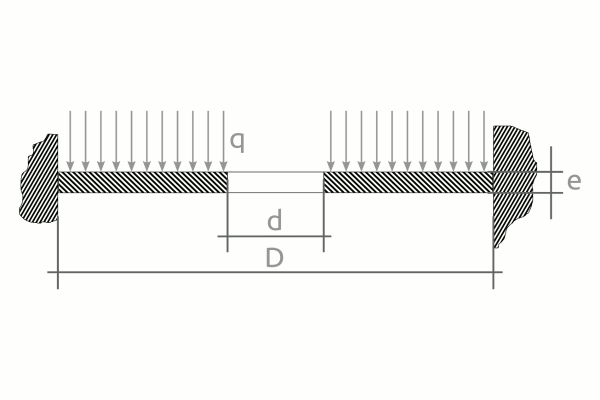
En particular nuestro caso, trata de una placa empotrada con una carga uniformemente distribuida, tal y como se aprecia en el siguiente croquis.

En todos los casos contemplados en el apartado 17 indicado anteriormente, la tensión máxima corresponde a:

$$ \sigma_{max} = k \times \frac{q \times (D/2)^{2}}{h^{2}} $$

mientras que la flecha máxima para:

se puede calcular a partir de:

$$ w_{max} = k_{1} \times \frac{q \times a^{4}}{E \times h^{3}} $$

donde,

• \( q \) es la carga en MPa
• \( D \) es el diámetro del disco en mm
• \( h \) es el espesor del disco en mm
• \( a = D/2 \)
• \( E \) es el módulo de Young en MPa, que para el acero es 210000 MPa

Los valores de \( k \) y \( k1 \), se pueden obtener en función de \( \beta \), de la siguiente tabla:

0.80		0.67		0.50		0.33		0.25		0.20
k	k1	k	k1	k	k1	k	k1	k	k1	k	k1
0.105	0.00199	0.259	0.0139	0.480	0.0575	0.657	0.130	0.710	0.162	0.730	0.175

donde \( \beta \) es:

$$ \beta = \frac{d}{D} $$

Estos valores se corresponden con el caso 10 de la tabla 3, del mismo apartado 17 Circular Plate with a Circular Hole at Center  del capítulo 3 Symmetrical bending of Circular Plates, del libro indicado anteriormente, Theory of plates and shells de Stephen Timoshenko y S. Woinowsky–Krieger, donde se definen igualmente los coeficientes \( k\ y\ k_1 \) para las ecuaciones indicadas anteriormente

Hay que tener en cuenta que según la norma ISO 5167-2, el diámetro d debe ser en todo los casos mayor o igual a 12,5 mm. La relación de diámetros β = d/D es siempre mayor o igual a 0,10 y menor o igual a 0,75. El valor de la razón β debe ser seleccionada entre estos límites.

Estas ecuaciones son válidas para un coeficiente de Poisson de:

$$ \nu = 0.3 $$

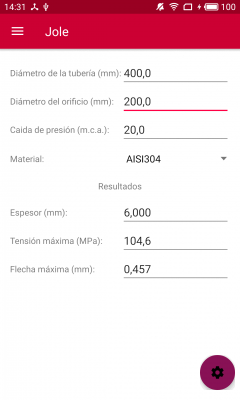
Por ejemplo, para el siguiente cálculo, en el que utilizaremos la aplicación Jole, resulta que necesitaremos un espesor para acero inoxidable AISI 304 de 6mm

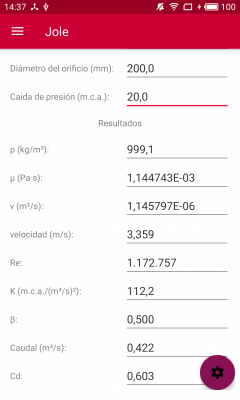
El caudal circulante con esas dimensiones y características de la placa de orificio, lo  calculamos igualmente utilizando Jole:

 

Si utilizamos un acero inoxidable, por ejemplo un AISI – 316, que corresponde a un acero grado 1.4401 según la norma UNE EN 10088-2, el límite elástico es de 220 MPa. Considerando un coeficiente de seguridad de 1,5:

$$ \gamma = 1.5 $$

$$ AISI\ 316 \Rightarrow \sigma_{max} = \frac{220}{\gamma} = \frac{220}{1.5}=146.37\ MPa $$

$$ \beta = \frac{200}{400} = 0.5 \Rightarrow k=0.48\ y\ k_1=0.0575 $$

El espesor necesario de placa sería el siguiente:

$$ h = \sqrt{k \times \frac{q \times (D/2)^{2}}{\sigma_{max}}} = \sqrt{0.48 \times \frac{0.196 \times (400/2)^{2}}{146.37}}=5.07\ mm $$

Tomando el espesor inmediatamente superior, e=6mm, la flecha máxima se determina a partir de la siguiente ecuación:

$$ w_{max}= k_{1} \times \frac{q \times (D/2)^{4}}{E \times h^{3}} = 0.0575 \times \frac{ 0.196 \times (400/2)^{4}}{210000 \times 6^{3}}=0.397\ mm $$

 

Conclusiones

Siguiendo este sencillo procedimiento hemos calculado, tanto utilizando Jole, como de forma manual el espesor mínimo necesario que necesitamos para la placa de orificio. Hay que tener en cuenta, que este espesor solo tiene en cuenta consideraciones mecánicas. Si nuestra intención es utilizar las placas de orificio para el cálculo del caudal circulante, además tenemos que tener en cuenta las consideraciones relativas al dimensionamiento indicadas en el artículo sobre el geometría de la placa de orificio.