No es algo habitual el cálculo de fondos para tubería de acero. Sin embargo, hace unos años, surgió la necesidad de instalar un fondo en una tubería. Concretamente en la obra del “Tramo E de la Conexión del Curso Bajo del Río Júcar con el Tramo V. Se trataba de una tubería de 1800 mm de diámetro y una presión de 4 MPa (40 atmósferas aproximadamente).
A continuación te detallaré los dos procedimientos utilizados. También te indicaré una solución muy sencilla que he implementado. Esta la puedes utilizar en caso de que necesites realizar el cálculo de un fondo para una tubería u otro elemento, como puede ser un depósito, etc.
Cálculo de fondos. Procedimientos.
Como he comentado en la introducción, para realizar el cálculo, utilicé dos procedimientos. Por un lado mediante elementos finitos y por el otro, utilizando la norma UNE EN 13445 Recipientes a presión no sometidos a la acción de la llama, Parte 3 Diseño.
CAELinux. Cálculo mediante elementos finitos
Para el caso del cálculo por elementos finitos utilicé el paquete de software libre CAELinux.
CAELinux es una distribución orientado al diseño asistido por ordenador. Esta distribución convierte tu equipo en una completa estación de trabajo con posibilidades para CAD, CAM, CAE, FEA y CFD. Pero con la ventaja de que no necesitarás ninguna licencia, al tratarse de software libre, y que además puedes hacerla funcionar directamente desde el propio Live CD. No necesitarás realizar ninguna instalación.
CAELinux está basada es software libre CAD/CAM como Freecad, LibreCAD, PyCAM y Cura. Mientras que, entre el software CAE que incluye puedes encontrar herramientas como Salomé, Code_Aster, Code_Saturne, OpenFOAM and Elmer. Con todas estas herramientas, tienes la posibilidad de diseñar y definir las geometrías mediante CAD y realizar cálculos mecánicos. Y en su caso, también podrás realizar cálculos hidráulicos.
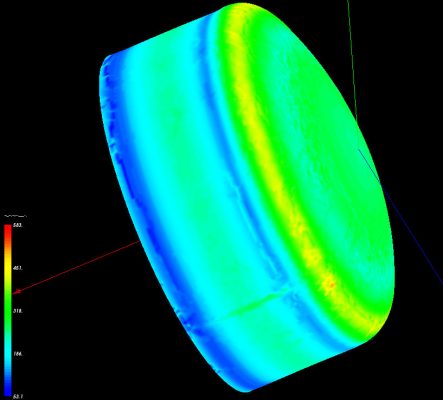
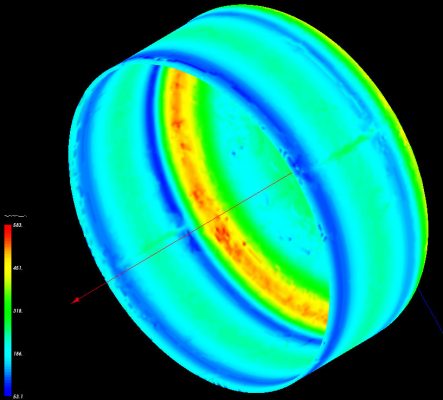
En el caso que nos ocupa, tan solo lo utilicé para realizar el cálculo mecánico del fondo, con la intención de comparar resultados. En la siguiente captura de pantalla, puedes ver el modelo en 3D,
A continuación, puedes ver un par de capturas de pantalla del resultado.
UNE EN 13445 Recipientes a presión no sometidos a la acción de la llama.
Dentro de la norma UNE EN 13445 se contemplan diferentes tipos de fondos, entre los que cabe destacar los fondos torisféricos. Y dentro de los fondos torisféricos tenemos,
- Tipo Kloepper donde \( \frac{R}{D_e} = 1.0 \) y \( \frac{r}{D_e} = 0.1 \)
- Tipo Korbbogen donde \( \frac{R}{D_e} = 0.8 \) y \( \frac{r}{D_e} = 0.154 \)
Además se deben cumplir las siguientes condiciones
$$ r \leq 0.2 \cdot D_i\\r \geq 0.06 \cdot D_i\\r \geq 2 \cdot e\\e \leq 0.08 \cdot D_e\\e_a \geq 0.001 \cdot D_e\\R \leq D_e$$
Procedimiento de cálculo
El espesor requerido e debe ser el mayor de los espesores \( e_s\ e_y\ e_b \), donde,
$$ e_s = \frac{P \cdot R}{2 \cdot f \cdot z – 0.5 \cdot P} $$
$$ e_y = \frac{\beta \cdot P \cdot (0.75 \cdot R + 0.2 \cdot D_i)}{f}$$
$$ e_b = (0.75 \cdot R + 0.2 \cdot D_i)\cdot[\frac{P}{111\cdot f_b}\cdot(\frac{D_i}{r})^{0.825}]^{(\frac{1}{1.5})} $$
Donde,
$$ f_b = \frac{R_{p0.2/T}}{1.5} $$
Salvo para los aceros austeníticos sin soldadura conformados en frío, en cuyo caso,
$$ f_b = \frac{1.6 \cdot R_{p0.2/T}}{1.5} $$
Por otro lado, la altura interior de un fondo torisférico viene dada por la ecuación,
$$ h_i = R – \sqrt{(R-\frac{D_i}{2})\cdot(R+\frac{D_i}{2}-2 \cdot r)} $$
Presión máxima admisible
Para una geometría dada, y para casos de carga de funcionamiento normal, la persión máxima admisible debe ser la más pequeña de las presiones siguientes,
$$ P_s = \frac{2 \cdot f \cdot z \cdot e_a}{R+0.5\cdot e_a} $$
$$ P_y = \frac{f \cdot e_a}{\beta \cdot (0.75 \cdot R + 0.2 \cdot D_i)} $$
$$ P_b = 111 \cdot f_b \cdot(\frac{e_a}{0.75 \cdot R + 0.2 \cdot D_i})^{1.5}\cdot(\frac{r}{D_i})^{0.825} $$
Ahora bien, se permite reducir el espesor de la parte esférica del fondo hasta el valor \( e_s \), en una zona circular cuyo borde no debe situarse a una distancia inferior a \( \sqrt{R \cdot e} \) de la parte tórica de la unión.
Ecuaciones de cálculo
$$ Y = min(\frac{e}{R}; 0.04) \\
Z = log_{10}(\frac{1}{Y}) \\
X = \frac{r}{D_i}\\
N = 1.006 – \frac{1}{6.2+(90 \cdot Y)^4}$$
- Para X = 0.06,
$$ \beta_{0.06}=N\cdot(-0.363\cdot Z^3+2.2124 \cdot Z^2-3.2937 \cdot Z+1.8873) $$
- Para 0.06 < X < 0.1,
$$ \beta = 25 \cdot [(0.1-X)\cdot \beta_{0.06}+(X-0.06)\cdot \beta_{0.1}] $$
- Para X = 0.1,
$$ \beta_{0.1}=N\cdot(-0.1833\cdot Z^3+1.0383 \cdot Z^2-1.2943 \cdot Z+0.837) $$
- Para 0.1 < X < 0.2,
$$ \beta = 10 \cdot [(0.2-X)\cdot \beta_{0.1}+(X-0.1)\cdot \beta_{0.2}] $$
- Para X = 0.2,
$$ \beta_{0.2}=máx[0.95\cdot(0.56-1.94\cdot Y-82.5\cdot Y^2);0.5] $$
Resultados
En la siguiente imagen puedes un fondo de diámetro 1.800 mm, instalado y punteado sobre la propia tubería a falta de realizar la soldadura.
 En esta otra imagen, se puede apreciar el fondo completamente soldado.
En esta otra imagen, se puede apreciar el fondo completamente soldado.
Aplicación Caps
Con el fin de facilitar el cálculo de fondos torisféricos del tipo Kloepper y Korboggen, he implementado una aplicación que puedes encontrar en el siguiente enlace Caps
Conclusiones
Como puedes ver el cálculo utilizando el procedimiento descrito en la norma UNE EN 13445 es relativamente sencillo. Tan solo tendremos que iterar hasta obtener los valores correctos. Desde luego, es mucho mas sencillo, rápido y práctico que realizar la modelización por elementos finitos.
Más información,
- UNE EN 13445 Recipientes a presión no sometidos a la acción de la llama.